Combinatoria

Tenemos un conocimiento intuitivo de probabilidad que nos conduce de forma inmediata a la idea de que la probabilidad de un suceso debe ser igual al número de casos favorables dividido entre el número de casos posibles. Así, por ejemplo, no nos cuesta entender que la probabilidad de obtener un 5 al lanzar un dado debe ser de 1 sobre 6. Es decir: 1/6.

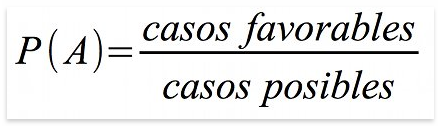
Los recuentos de casos favorables o posibles en ejemplos tan sencillos no precisan de técnicas complejas. Sin embargo, si en lugar de lanzar un dado lanzamos dos dados y hacemos la misma pregunta la cuestión ya se complica un poco y nos obliga como mínimo a diseñar una tabla como la siguiente:

	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

Por tanto la probabilidad es de 4 casos favorables sobre 36 posibles. Claro que si seguimos añadiendo dados a nuestro experimento, el recuento de casos posibles llega a complicarse tanto que podría ser inabordable. Por ello tendremos que recurrir a técnicas de recuento más fiables y rápidas. De ahí, la necesidad de incluir la combinatoria como paso previo a la probabilidad.